今日聚焦

含义解读

流动性陷阱指当名义利率降低到无可再降低的地步，甚至接近于零时，由于人们对于某种“流动性偏好”的作用，宁愿以现金或储蓄的方式持有财富，而不愿意把这些财富以资本的形式作为投资，也不愿意把这些财富作为个人享乐的消费资料消费掉。国家任何货币供给量的增加，都会以“闲资”的方式被吸收，仿佛掉入了“流动性陷阱”，因而对总体需求、所得及物价均不产生任何影响。

因此，经济学家将利率已经降到极低水平时，单单依靠调整货币政策无法达到刺激经济的目的，极低的利率和国民总支出水平不会发生变动的状况称为“流动性陷阱”。百度百科如下：

https://baike.baidu.com/item/流动性陷阱/3489234?fromtitle=流动偏好陷阱&fromid=9788871&fr=aladdin

高鸿业西方经济学第六版 宏观部分对“流动性陷阱”的讲解如下，原书P432：

这里需要解释一下，因为债券价格与利率成反比，所以当利率（这里代指债券的到期收益率）越低，债券价格越高。当利率低到极限时，此时债券价格也会高到极限了。这时候人们认为利率都这么低了，肯定已经低到极限了，未来不可能再下降了，一定要开始上升了。又因为利率与债券价格成反比，因此人们也就认为债券价格都高到这么离谱了，一定已经高到天花板了，未来不可能再继续高了，一定会开始价格下跌了。

因而人们都不看好未来债券的价格，都预期未来债券价格一定会持续下跌（利率持续上升），因此都纷纷不看好未来的债券，因此都会将现在手上所持有的所有债券都赶紧换成现钞攥在手心里，来让自己放心。这时候，即使人们手里有了越来越多的现钞，人们也会将它们都仅仅攥在手心里，或者藏在枕头下，绝不会拿这些钱去买债券了。以免债券未来价格下跌时会遭受损失。

即无论增加多少货币，都会被人们储存起来。发生流动性陷阱时，再宽松的货币政策也无法改变市场利率，使得货币政策失效。国民手中的钱袋就像是一个能够吸收任何物质的“黑洞”一样，把国家分配给国民的所有货币都无情地吞噬掉了，由此产生了一个货币需求无限大的“流动性陷阱”。国家任何货币供给量的增加，都会以“闲资”的方式被吸收，因此政府通过任何货币政策来增加货币供给，进而刺激经济的行为都无法奏效。

形成原因

①根据货币需求理论，利率是持有货币的机会成本。也就是说，当人们没有用有利息的债券来持有财富时，就失去了本来可以赚到的利息。当利率很低的时候，持有货币的成本就降得很低。
②利率下降会导致投机性货币增加。当利率降低到一定程度时，即意味着生息债券的价格已经很高，存在极大下跌的风险。此时人们对经济情形判断悲观，认为债券价格只会下降不会上升，因此停止买入债券。同时预期利率上行，将货币留在手中，留至下次投机使用。
③同时，货币是最具流动性的资产，转换成其他经济媒介的难易程度最低。人们会依据流动性偏好（也被称为货币需求）的3种动机，即交易动机、谨慎动机、投机动机选择持有货币，以及时地转换成其他物品和劳务。

主要表现

从宏观上看，一个国家的经济陷入流动性陷阱主要有三个表现：
(1)整个宏观经济陷入严重的萧条之中，需求严重不足，居民个人自发性投资和消费大为减少，失业情况严重，单凭市场的调节显得力不从心。
(2)利率已经达到最低水平，名义利率水平大幅度下降，甚至为零或负利率，在极低的利率水平下，投资者对经济前景预期不佳，消费者对未来持悲观态度，这使得利率刺激投资和消费的杠杆作用失效。货币政策对名义利率的下调已经不能启动经济复苏，只能依靠财政政策，通过扩大政府支出、减税等手段来摆脱经济的萧条。
(3)货币需求利率弹性趋向无限大。

总结

总结一句话，我们说，决定一个国家经济走势的最根本的因素是该国家的老百姓的信心和斗志，如果一个国家的所有人都丧失了精气神，都萎靡不堪，那么一个国家的经济必然走向萧条，各行各业都丧失了干活的斗志，必然引起经济萧条。凯恩斯流动性陷阱就是当人们对未来经济前景完全不抱任何希望时，政府任何的货币政策都无法刺激人们的干劲，从而导致政府投入的大量货币现钞都只是进入了人们的钱袋子里，人们把钱藏在床底下，而不会因有这笔钱而变得信心大增，斗志高昂。所以会产生这种“凯恩斯流动偏好陷阱”。因此不论是财政政策也好，还是货币政策也好，根本目的都是为了激发广大人民群众的干劲和精气神，只要大家心往一处想，劲往一处使，再困难的经济局面都能得到改观，就没有过不去的经济危机。

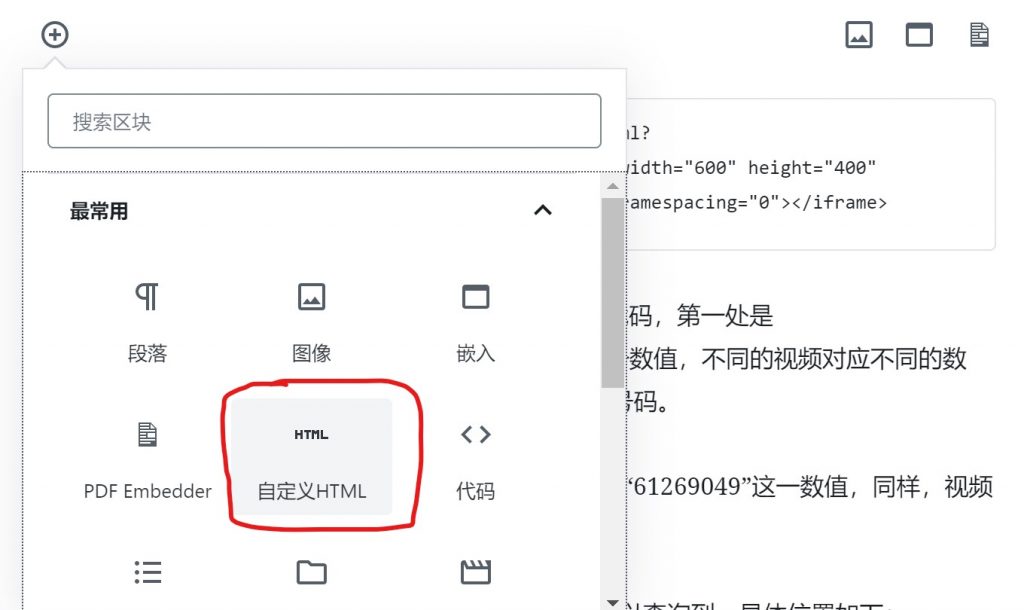
由于B站里内置的分享模块中给定的视频内嵌html代码在WordPress上视频尺寸显示过小，影响观看，因此博主今天和大家分享一个内嵌B站视频的一个简单好用的方法。

使用本方法嵌入视频，首先要进入文章编辑器的自定义html选项：

接着在自定义html中输入如下代码：

<iframe src="//player.bilibili.com/player.html?aid=34972664&amp;cid=d=61269049&amp;page=1" width="600" height="400" scrolling="no" border="0" frameborder="no" framespacing="0"></iframe>

其中，对于不同的视频，需要修改两处上面的代码，第一处是 aid=34972664&amp 这部分的“34972664”这一数值，不同的视频对应不同的数值，aid=的数值是B站的分享模块中出现的aid号码。

第二处是 cid=d=61269049&amp 这部分的“61269049”这一数值，同样，视频不同，cid数值也不同。

以上aid与cid两处数值，在B站的分享模块中可以查询到。具体位置如下：

使用该方法嵌入视频后的效果如下所示：

完全替代品的indifference curves的斜率不是必须为-1的，也可能等于-2，-5，-10000，都有可能的。

完全替代品是指两种物品间的替代比例是固定不变的情况，相应的无差异曲线为一条斜率不变的直线，MRS12为一常数。比如1元硬币和5角硬币，无论组合中的1元硬币和5角硬币有多少，你总愿意用1枚1元硬币换2个5角硬币。你在1元硬币和5角硬币之间的边际替代率是一个不变的数——2。再比如，对有些人来说，可口可乐和百事可乐也属于完全替代品，它们之间的替代率总是1∶1。

对于完全替代品来说，其无差异曲线的斜率不一定等于-1。例如，丹认为一片16兆的存储芯片与两片8兆的存储芯片一样，因为这两个芯片组合的存储容量是相等的。如果是那样的话，丹的无差异曲线的斜率将会是-2（假如纵轴表示8兆存储芯片的数量）

一般情况下，完全替代偏好的的效用函数表达式是:U(X1，X2)=aX1+bX2,U(X1，X2)代表消费者从商品1、商品2获得的效用，X1/X2表示两种商品的数量，a、b表示消费者对商品1、2的价值判定，其无差异曲线的效率是-a/b。例如对于消费者来说商品1的价值是商品2的2倍，因此得到U(X1，X2)=2X1+X2，其无差异曲线的斜率就是-2。注意：在利用完全替代品公式时，X1、X2所代表的是商品数量，所以其数量乘以所蕴含的价值才等于效用。

完全替代品的需求函数，主要考虑价格因素，在两种商品可以完全替代的情况下，消费者肯定会选择价格便宜的那一种，其需求函数为：
m/p1 若p1p2 X1是商品1的需求数量，p1、p2定代表商品1、商品2的价格，m代表消费者的收入。

完全替代品的需求变动完全是替代效应在起作用，收入效应为零。

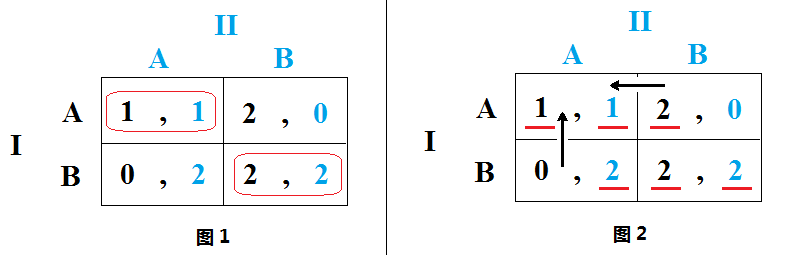
一个博弈有可能存在很多个纳什均衡，对纳什均衡的精炼就是以不同的标准剔除在某一衡量标准下相对不合理或不稳定的纳什均衡而筛选出最合理或稳定的纳什均衡， 这个过程叫做纳什均衡的精炼(refinement)。

颤抖手均衡是纳什均衡的一种精炼, 简单地说， 在一个纳什均衡状态，如果其中一个参与者的手颤抖了一下（假设为小概率事件）选择了次优的策略，那么一个纳什均衡是颤抖手均衡的要求就是参与者有动机重新回到原来的均衡，而不是这个偏离并趋向另一个纳什均衡。

如上图的例子， 图1显示这个博弈有两个纯策略纳什均衡，（A, A） 和 （B,B）, 收益分别是 （1，1） 和 （2，2） ；但颤抖手均衡只有一个，就是（A, A），收益为（1，1）。解释如下：

假设双方处于（A, A）这个纳什均衡， 如果参与者 I 颤抖，选择了B, 那么博弈的结果是 （B, A）,在 （B, A）, 参与者 I 有动机改变现状，因为选B的收益是0， 而选A的收益是1， 所以参与者 I 会重新选择A, 使博弈回到（A, A）这个均衡，对参与者 II 来说，（B,A）和（B,B）的收益是一样的，都是2，所以在（B,A）参与者II 没有动机改变现状。综上， 在（A,A）这个均衡，颤抖后博弈会重新回归这个均衡。直观地说（A,A）是抗震的，震完以后会归位。（A,A）就是一个颤抖手均衡。
相反，（B,B）就不是一个颤抖手均衡。

假设双方处于（B,B）, 收益 （2，2），如果有参与者颤抖，比如参与者II 颤抖到A，博弈结果成为（B, A）,收益变成 （0，2），在这个情况下，对于II 来说没有动机改变，因为颤抖前后收益都为2, 但对于I 来说，就不一样了，如果II 颤抖到A, I 的收益就从2变到0， 如以上所述，在（B,A）的情况下，I 有动机改变并选A。 所以，在(B,B)这个纳什均衡点，颤抖后均衡会趋向 （A,A）这个点，所以(B,B)就是在颤抖情况下不稳定的， （B,B）就不是一个颤抖手均衡。

在只有两个参与者的情况下，颤抖手均衡的一个充分必要条件是：是纳什均衡并且没有一个参与者的策略是弱劣策略（weakly dominated）。如图的列子里，B 对双方来说都是弱劣策略，所以根据这个充要条件，(B,B)可以被简单地剔除。

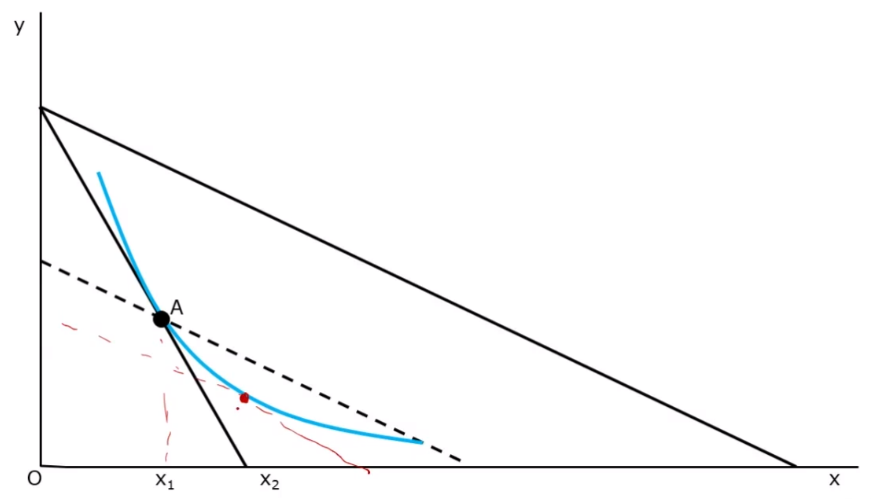
关于希克斯分离法的详细解读参见另一篇博文 收入效应与替代效应（采用了希克斯方程分离两种效应，斯勒茨基方程请见另一篇文章）

斯勒茨基替代效应是指在商品价格变化后，在保持消费者实际收入不变（这里的实际收入不变是指消费者在价格变化后能够购买他想要购买的价格变化以前的商品购买量，即实际购买力不变）的情况下所引起的商品需求量的变化。

斯勒茨基收入效应是总效应减去替代效应后的部分效应，是由于收入变动所引起的纯效应。当收入固定而商品1的价格发生变动时，预算线绕纵轴转动。我们把这种调整看作是分两阶段发生的：首先是转动，即预算线绕原来选择的商品束转动；然后是移动，即这条转动后的线向外移动到新的需求约束上。

希克斯与斯勒茨基的唯一不同之处在于对替代效应的分离手法不同，即对于保持消费者实际收入不变这一概念的理解上不同，希克斯认为， 消费者在价格变化前后保持在同一条无差异效用曲线上，即为保持了消费者实际收入不变，即实际收入不变=实际效用不变。斯勒茨基则认为，只有保证消费者的收入（即实际购买力）不变，即消费者在价格变化后，仍有和价格变化前相同的购买能力，才是真正保持了消费者实际收入不变。

希克斯替代效应是和斯勒茨基替代效应是对于价格效应的不同解释。希克斯替代效应是指在商品相对价格发生变化后，在保持消费者实际收入不变（这里的实际收入不变是指消费者在价格变化前后保持在同一条无差异曲线上）的情况时下所引起的商品需求量的变化。而斯勒茨基替代效应指的是在商品相对价格发生变化后，在保持消费者实际购买力不变（这里的实际购买力不变是指消费者在价格变化后能够购买他想要购买的价格变化以前的商品购买量 ）的情况时下所引起的商品需求量的变化。

不论是希克斯还是斯勒茨基，其分离法的核心和第一步，也是首要任务，都是对替代效应进行分离。然后所谓的收入效应就是总效应减去替代效应之后，所剩下的效应。

通过这两种分离手段，得出的总效应是相同的，二者的区别是替代效应与收入效应各自所占总效应的比例有所不同。

下面来看一下斯勒茨基（slutsky）与希克斯（Hicks）分离法的区别，下图红色虚线部分是希克斯分离法。

希克斯分离法的目标是确保消费者的效用水平不发生变化，仅仅改变商品的相对价格，即改变预算线的斜率，从而观察替代效应——保持效用水平不变，由于商品价格变化而导致的对该商品消费量的变化。

而slutsky分离法是这样的，如下图黑色虚线所示，它的目标是在新的商品价格关系下，使消费者仍然买得起原来的消费组合数量（即A点），即保持消费者的实际购买力不变，只去改变两种商品的相对价格，从而观察替代效应——保持实际购买力不变，由于商品价格变化而导致的对该商品消费量的变化。

如上所述的不同，是希克斯分离法与斯勒茨基分离法的唯一不同之处。

下面继续看斯勒茨基分离法。如下图所示，黑色虚线与新的无差异曲线相交于B点。

然后我们接下来可以把图划分成3部分，如下图所示。当X1增加到X2时，是替代效应。

当商品为正常品时

如果消费量增加了，且最终增加到超过x2的数量水平，那么该商品就是正常品。如下图。（即当替代效应和收入效应都是正数时，此时该商品为正常品，其中x1到x2的增长是因为替代效应，x2到最终的x值这一部分是由于收入效应）

当商品为普通劣等品时

如果变化到下图所示，则该商品为普通劣等品。（即收入增加后，X的消费量减少了，但是并没有减少到超过替代效应，即收入效应导致的消费的减少量比替代效应导致的消费增加量要小，因此总效应还是增加的，但是增加的幅度不会很大，此时该商品为普通劣等品）。此时收入效应<替代效应。

当商品为吉芬商品(Giffen Good)时

如果收入效应很大，大到超过了替代效应，且收入效应为负数，则总效应也是负数，那么该商品为吉芬商品。

拓：吉芬商品

吉芬商品是指某种生活必需品，在某种特定的条件下，消费者对这种商品的需求与其价格成同方向变化。即价格越涨，买的人越多。价格越下降，买的人反而变少了。吉芬商品首先一定是劣等品。

吉芬物品是一种特殊的低档物品。作为低档物品，吉芬物品的替代效应与价格呈反方向变动。吉芬物品的特殊性就在于，它的收入效应（为负数）的作用很大，以至于超过了替代效应的作用，从而使总效应与价格呈同方向变动。这也就是吉芬物品的需求曲线呈现出向右上方倾斜的特殊情况的原因。

吉芬物品首先必须是劣等物品（Inferior good），并且是可以被替代的，在静态的价格需求曲线上，随着价格和需求同升同降的商品。

但是吉芬物品与其说是一种商品，不如说是一种现象，到底什么才是吉芬物品，正确的吉芬品例子如下：对于过去的西方人来说，土豆是一种廉价的主食，当土豆和其他食物、比如肉类的价格恒定的时候，穷人消费土豆的量是一定的，但是一旦土豆价格下降的时候，由于土豆变便宜了，所以花比原来更少的钱就可以买到和原来一样多的土豆，穷人的生活一般来说是没有什么结余的，由于土豆降价了，他们就没必要买原来一样多的土豆，这个时候他们很可能会选择减少土豆的需求量，凑钱去购买比土豆昂贵的替代品（比如，原来一天只吃十个土豆正好吃饱，现在土豆降价了，只买八个，剩下的钱，正好可以买一块肉回家，当然买十个土豆也能剩下些钱，但肯定比八个土豆情况下买的少，而且一样正好吃饱肚子，又不会因为吃十个土豆再加肉而吃撑），由于静态下需求曲线是可逆的，在这个瞬间，土豆要是价格反弹，那么穷人马上回到原来的消费结构上去。这才是真正意义上的吉芬物品！但是土豆的这种价格同需求的同方向移动现象并不是一直存在的，确切的说，应该是需求曲线的某一段产生了向上的现象，也就是说当土豆价格高到一定程度，需求又开始下降，因为这个时候穷人连土豆都吃不起了。所以吉芬物品并不是指其需求曲线永远向上，而是需求曲线带有这种反常现象的商品。

吉芬物品比较不常见，历史上有一个经典的例子：1854年爱尔兰发生大饥荒而使马铃薯的价格大幅度上涨之时，对马铃薯的需求量却反而增加了。这是因为当时人们太穷了，平时人们所能消费得肉类便不太多，如今马铃薯涨价了，相对他们来说更穷了，穷到买不起原本消费肉类的数量，结果只好增加对马铃薯的购买来补救。

下面是斯勒茨基方程的解读，总效应是收入效应和替代效应之和。

该方程有三个重要的点，如下图所示。分别是最初的均衡点A，最终的均衡点，以及补偿预算线上的均衡点B。

下面对最初的均衡点A进行解读。两商品的消费量决定函数为X(Px, Py, m)，其中m为总预算金额。Px为商品x的售价，Py为商品y的售价。

下面是最终的均衡点的解读。此时价格变化后的两个商品的消费量决定函数为X(Px’, Py, m)。因为总预算金额没有改变，改变的仅是x商品的售价，y商品的售价并未改变，因此三个变量仅有Px减小为Px’，其余两个自变量没有变化。

最后是位于补偿预算线上的均衡点B的解读，如下图所示。在B点，两商品消费量的决定函数变为X(Px’, Py, m’)。注意，此时由于是在补偿预算线上，因此预算金额m也变小为m’了）

下面分析斯勒茨基替代效应与收入效应的表示方程。如下图所示：

斯勒茨基替代效应 ΔXs= X(Px’, Py, m’) – X(Px, Py, m) ，即用补偿预算线上的均衡点B减去最初均衡点A。

斯勒茨基收入效应 ΔXn= X(Px’, Py, m) – X(Px’, Py, m’) ，即用最终均衡点减去补偿预算线上的均衡点B。

所以得到斯勒茨基方程的总效应为

ΔX= ΔXs（替代效应） + ΔXn （收入效应）

= X(Px’, Py, m’) – X(Px, Py, m) + X(Px’, Py, m) – X(Px’, Py, m’)

=X(Px’, Py, m) – X(Px, Py, m)

其中上式中加粗斜体部分相加的和为0，因此可以直接省略掉。

悉达多老师版课件中的斯勒茨基方程形式为：

•Δx =[x(Px2,m2)-x(Px1, m1)]+[x(Px2, m1)-x(Px2,m2)]

=x(Px2,m1)-x(Px1, m1)

即最终均衡点减去最初均衡点A。

解读收入效应为负数的情形

本质上就是当该商品为劣等品时（因为吉芬商品也属于劣等品的一种，只是一种特殊情况下的劣等品，即吉芬商品是收入效应（负数）完全大于替代效应（正数）时的一种商品），随着该商品价格下降，导致消费者实际购买力增强时，消费者会赶紧减少该商品的需求。

就像流浪汉没钱时会吃窝窝头，当他有钱了，他看都不想看窝窝头一眼，更不想多买窝窝头了，因此他会大量减少窝窝头的购买量，因为窝窝头是劣等品，等有钱了流浪汉才不会再去多买它吃。即实际收入增加，消费者反而不想去买的商品，就是劣等品，他的收入效应为负数。

本文内容来源于博迪投资学中文第10版的第149-151页，“附录6A 风险厌恶、期望效用与圣彼得堡悖论”相关内容。在此，博主谈谈对这部分内容的理解。以下为原书书影。

该问题的核心解答是人们对于每一单位新收益的边际效用是递减的（特别是，他们的财富越多，对每额外增加的美元赋予的“价值评级”就越少），意味着随着游戏次数的增加，每一单位新的收益所带来的效用不断递减，最后几乎为0，所以当游戏次数趋于无穷，总效用也会趋于一个稳定值，而不是无限增长。因此将这个稳定的效用值转换成他的效用函数里所对应的金额，就是这个玩家所愿意付出的最高门票金额，因为只有当U（门票钱）＜U（游戏所得收入）时，他才会去玩这个游戏。这样对玩家来说才有利可图。一旦当U（门票钱）＞U（游戏所得收入），他不会去参加这个游戏，他宁愿攥着本来用于购买门票的钞票回家睡大觉，也不想去参加这个游戏了。因为这时在效用上，他是亏本的。

所谓“悖论”，是因为根据计算，这个游戏的收益是随着游戏次数的增加而无限制增长的，所以人们按理说应该无限制地把这个游戏玩下去的，但是实际生活中，人们一般玩上几次就不玩了，所以这造成了一个矛盾的存在，这就是所谓的悖论。原因是每次玩，门票费用也是在增加，因此人们不会无限制地玩下去的。

上面有句话很难理解，就是为啥说“这个游戏的主观效用值确实是有限的，等于0.693”。这句话的意思是，玩一次这个游戏就能扔到正面的期望效用值为（1/2）*ln（2^0)，玩两次这个游戏才能扔到正面的期望效用是（1/2^2)*ln(2^1), 玩3次这个游戏才能扔到正面的期望效用是（1/2^3)*ln(2^2)。

所以，预期报酬为:

一个特殊的函数ln(R)分配给报酬为R美元的投资者一个主观的价值，报酬越多，每个美元的价值就越小。如果以这个函数衡量财富的效用值，那么这个游戏的主观效用值确实是有限的，等于0.693，即：

获得该效用值所必须的财富为2美元，因为ln(2)=0.693，因此风险报酬的确定等价物为2美元，也是投资者愿意为游戏付出的最高价钱。

以上内容详细叙述了“圣彼得堡悖论”的来龙去脉。这个问题的核心是探讨游戏参与者愿意为玩这个游戏所付出的最高价钱是多少。下面的例子讨论了“风险厌恶”的基本原理和公平博弈。

关于风险厌恶者，风险喜好者和风险中性者的对比，详见本博客的另一篇文章：风险厌恶者，风险中性者和风险喜好者的区别

下面的内容详细讨论了风险厌恶和期望效用的关系。

在这里主要谈一下文章最后一部分，最后一段里，为什么说“投资者认为稳拿的86681.87美元与有风险的100000美元的效用值相等”。

因为这里计算的风险投资的期望效用11.37，即：

这个11.37，是这种游戏本身所值的效用值，它也并不是独立于游戏玩家之外的客观存在。决定它的大小的因素来源于游戏玩家的心理偏好。大家可以看到，这个11.37在一条笔直的斜线的中点处，这条斜线的两个端点则都在游戏玩家的自身效用曲线上，在中点则意味着这个11.37是一个算数平均值，是这两个端点的平均值。因此，11.37并不是单纯由玩家的效用函数生成的效用值。它虽然与把
86681.87美元带入效用函数（即ln(86681.87美元)=11.37效用)所得到的效用的结果相同，但是它的来源并不是来自于86681.87美元，而是来源于 0.5*ln(50000)+0.5*ln(150000)=11.37 。换言之，它来自于公平博弈游戏所带来的两种游戏结果的效用的平均值。这颇有点“青出于蓝而胜于蓝”的味道。11.37出之于50000美元的效用值和150000美元的效用值的平均值，它源于效用函数，而又不同于效用函数所生成的效用值。

那么11.51又是啥呢？

这里的11.51，是ln（100000）的计算结果，如下所示：

这是将100000美元的财富放置于玩家自身效用曲线上所得到的效用值，换言之，玩家不是把这100000美元投于玩这个公平博弈游戏， 而是持有这100000美元啥都不干所带来的“快感”值11.51。所以在这种情况下，在效用函数为凹函数的情况下（即随着财产数量的增加，每个单位的价值递减；关于为什么风险厌恶者的效用函数为凹函数，参见风险效用函数）。

换言之，玩家选择不参加这个玩心跳的游戏，而是手握这100000元钱在家躺着睡大觉的效用值为11.51，而选择参加这个胆战心惊的游戏，所获得的期望效用为11.37（即平均来说，参加这个游戏所获得的效用值为11.37）。那么，结果一目了然了。也即是说，在风险厌恶者看来（即效用函数为凹函数的人看来），玩这个游戏一点儿也不划算，效用值还不如不玩这个游戏，而选择躺在家里睡大觉的效用值高。所以说，风险厌恶者不会参加公平博弈。

这里的11.37同时位于一条斜率确定的斜线的中点上，也就是说，11.37是一个算数平均值，是ln（50000）与ln（150000）的平均值，也就是平均来说，玩这个公平博弈游戏所能收获的效用值为11.37。

那么现在还有一个问题，那就是算出了平均来说，玩这个公平博弈游戏所可能获得的效用值为11.37，那么把这个11.37置于玩家自身的心里偏好曲线，即这个凹函数曲线上，此时ln(Wce)=11.37，所对应的财富值为Wce=e的11.37次方=86681.87美元。注意，这个11.37的效用值意味着，玩家选择不玩游戏，而是手里攥着86681.87美元去睡大觉的效用值是11.37，它等于玩家选择铤而走险，拿着100000美元去参加这个令人心跳不止的公平博弈游戏所带来的平均效用值。也就是说，玩家选择手里攥着86681.87美元在家里躺着睡大觉的效用与拿着100000美元去参加公平博弈游戏所获得的效用是相等的。

所以书本中最后一句话才会说道 “投资者认为稳拿的86681.87美元与有风险的100000美元的效用值相等 。因此，对他来说二者没有什么区别。”

结尾附上著名华裔经济学家黄有光教授于1965年发表的推翻“阿罗不可能定理”的论文。 Ng, Yew-Kwang (1965). “Why Do People Buy Lottery Tickets? Choices Involving Risk and the Indivisibility of Expenditure”

Kwang-1965-Why-do-people-buy-lottery-tickets-c