在时间序列的统计分析中,趋势平稳过程是一个随机过程 (stochastic process)。这意味着,可以从中除去潜在的趋势(趋势仅是时间的函数),而剩下一个平稳的过程。趋势不必是线性的。总之,趋势平稳的概念不如平稳性概念严格,有些过程非平稳,但却是趋势平稳的。
相反,如果一个过程在差分后变平稳了,则称该过程为差分平稳 (difference stationary),该过程有一个或多个单位根。趋势平稳和差分平稳两个概念有时可能会混淆,尽管它们有许多共同的属性,但在许多方面有所不同。一个时间序列可能是非平稳的,但该时间序列却没有单位根,并且它是趋势平稳的。在单位根和趋势平稳过程中,均值会随着时间的推移增加或减少。 但是,在发生冲击的情况下,趋势平稳过程是均值恢复的(即遭受冲击只是暂时的,时间序列将再次趋向于不断增长的均值,而不受冲击影响),而单位根过程则对均值具有永久性的影响(即随着时间的推移没有收敛)。
正式定义:
如果过程{Y}被认为是趋势平稳的,那么有
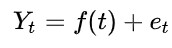
其中t是时间,f是从实数到实数的任意函数的映射,并且{e}是固定过程。值 f(t) 被认为是该过程在时间t的趋势值。
最简单的例子:线性趋势周围的平稳性
假设因变量Y满足如下等式
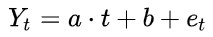
其中t是时间,et是误差项,假设et是白噪声过程,或更一般地说,et是由任何平稳性过程生成的。然后可以使用线性回归来获得时间趋势t的斜率 α 的估计值 α-hat,和截距项 b 的估计值 b-hat ; 如果估计值 α-hat 明显不为0,这足以在高置信度下表明变量Y是非平稳的。该回归的残差的估计量 et-hat 为
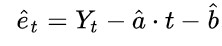
如果这些估计的残差可以从统计学上证明是平稳的(更确切地说,如果人们可以拒绝“真实的残差是非平稳”的假设),则这些残差称为去趋势数据 (detrended data) 。此时,尽管原始序列 {Yt} 是非平稳的,但称它是趋势平稳 (trend-stationary) 的。
本文基于以下文章撰写:
https://en.wikipedia.org/wiki/Trend-stationary_process


评论前必须登录!
立即登录 注册