总括具体的三大步骤:
- 删除第一个矩阵中的特定行(如第一行,第一行对应着第一个结构方程)。
- 选择与您已删除的行中具有零的元素相对应的列。
- 如果在从列数组创建的子矩阵中有(g-1)行或 (g-1) 列不全为零,其中g是内生变量(Y1, Y2, Y3)的数量,并且列和行是线性独立的,则方程为 identified。也就是说,只要在所新建的子矩阵中,有 (g-1)行或 (g-1) 列不全为零,则该方程为identified。比如结构方程组中,内生变量共有Y1, Y2, Y3等三个,所以g = 3,那么,只要新建的子矩阵中有(3 – 1)= 2 行或者2 列不全为0,则该方程为identified,否则一律都按not identified来算。举例如下:

Example: Identification in Equation 1
1)删除第一行
2)选择与Y2,Z2所对应的列(因为在方程1,即矩阵的第一行中,只有Y2与Z2元素的系数为0)
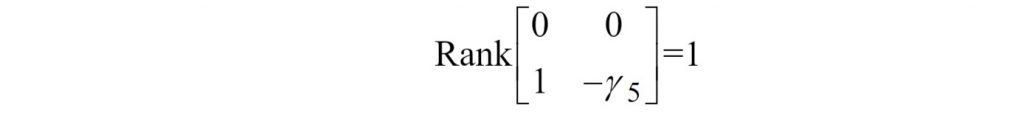
3)由于只有1行具有非零元素(新建的子矩阵结果如上,可以知道该子矩阵的秩为1),因此第一个方程为 not identified。 换句话说,在第一个方程中,当且仅当不全为0的行数为 (g – 1)行,也就是 3 – 1 = 2 行时,该方程才能是identified的,只要不是这样,就一律称该方程为 not identified,由于子矩阵的不全为0的行数只有1行,不满足identified的要求,因此称方程1为 not identified 。
Example: Identification in Equation 2
1)删除第二行
2)选择第二行中与零相对应的列,则新建的子矩阵如下:
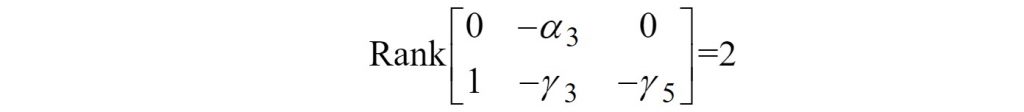
3)由于有两行具有非零元素,因此方程2为identified 。 换句话说,在第二个方程中,当且仅当不全为0的行数为 (g – 1)行,也就是 3 – 1 = 2 行时,该方程才能是identified的,只要不是这样,就一律称该方程为 not identified,由于子矩阵的不全为0的行数为2行,恰好满足了identified的要求,因此称方程2为identified。
Example: Identification in Equation 3
1)删除第三行
2)选择第三行中与零相对应的列。则新建的子矩阵如下:

3)由于子矩阵中有两行具有非零元素,因此方程3为identified 。换句话说,在第三个方程中,当且仅当不全为0的行数为 (g – 1)行,也就是 3 – 1 = 2 行时,该方程才能是identified的,只要不是这样,就一律称该方程为 not identified,由于子矩阵的不全为0的行数为2行,恰好满足了identified的要求,因此称方程3为identified。


评论前必须登录!
立即登录 注册