谈到多元函数可微与可偏导时,相信不少人头皮有点发麻。一元函数中,可微与可导是等价的,但是在多元函数中,可微与可偏导之间的关系就没那么简单了,这是为什么呢?本文小编将以二元函数为例进行详细的说明。
1.二元函数的可偏导
在二元函数中,一元函数的可导的概念变为可偏导,导函数的概念变为偏导函数,具体看下例:
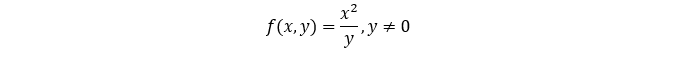
二元函数f(x,y)对x、y的偏导函数分别为:

在求二元函数的偏导函数时,都是假设另外一个变量为常量,然后对余下那个变量求导数。例如,f(x,y)对x的偏导函数,就是假设y为常量,然后f(x,y)对变量x求导数即得。
对于某一点,函数f(x, y)在该点的两个偏导数可能都存在、可能只存在一个、也可能都不存在。
在点(0, 0)的两个偏导数只存在一个的函数例子:

在点(0, 0)的两个偏导数都不存在的函数例子:

在点(0, 0)的两个偏导数都存在的函数例子:

对于上面三个例子,小编建议大家亲手去算算偏导数,这样能加深对二元函数偏导数的理解。
2.二元函数的可微
某一点可微描述的是函数增量与自变量增量之间的线性关系。在一元函数中,若线性主部的系数只与该点有关,则可微。以此类推,在二元函数中,若多个自变量的线性主部的系数都只与该点有关,则可微。下面分别列出一元函数、二元函数函数增量与自变量增量之间的关系式:

对于一特定点,当A、B为常数时,即A、B与自变量增量无关,则函数在该点可微,且A、B分别为函数在该点对x、y求偏导后的偏导数。
3.可微、可偏导、连续、导函数连续之间的关系
为了方便比较一元函数,小编先给出一元函数在某点C上关于可微、可导、连续、导函数连续的关系图。在图1中,函数f(x)可微与可导等价,因此可微与可导之间是双向箭头;在点C可微、可导必能得出函数f(x)在点C连续,但连续不能推出f(x)在点C可导、可微。因此可微、可导与连续之间是单向箭头。而导函数在点C连续,很明显就能推出函数在点C可导、可微、连续,但反过来,无法推出导函数在点C连续。

图1.一元函数可微、可导关系示意图
小编提醒大家,一定要经常记忆上图,而且是要理解性地记忆,比如说一元函数可微,要能明白可微是什么,关系式如何写!
相比于一元函数,二元函数就复杂多了,下面先给出二元函数可微、可偏导、连续、导函数连续的关系图。

图2.多元函数可微、可偏导关系示意图
当然在记忆这些关系时,我们通常要花时间记忆的是那些不容易理解的关系,而这些不容易理解的关系是与一元函数相比较后的那些不同之处。
3.1可微与可偏导不等价
在阐述二元函数可微与可偏导不等价前,不妨先回顾下,为什么一元函数中可微与可导是等价的?
在一元函数中,如果函数f(x)在x=x0处可导,则有如下关系式:
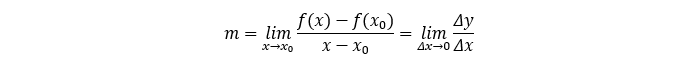
假设在一元函数中,函数增量与自变量存在如下关系:
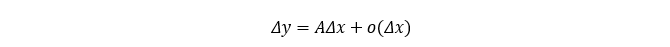
上式两边同除以△x,然后两边对△x取极限,可知A=m,则根据一元函数可微的定义,A只与x=x0有关,与△x无关,所以f(x)在x=x0可微。同理,不难得出在一元函数中,可微亦可推出可导。
那么在二元函数中,如何论证可微必可推导呢?
假设二元函数在点C(x0, y0)可微,则由可微的定义,必存在(x0, y0)的某邻域,使得下式成立:

不妨分别令△x=0、△y=0,根据①式可得:
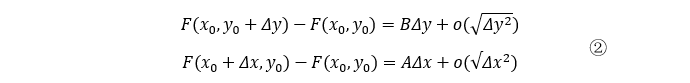
之所以可以令△x=0、△y=0,是因为点(x0, y0+△y)和(x0+△x, y0)都在点(x0, y0)的可微邻域内。
对②中两式求极限,可得:

结合偏导数的定义和③中的两个极限,可知可微情况下,函数在点C的两个偏导数都存在,因此可微必可偏导。
尽管可微必可偏导,但反过来不成立,请看下面这个例子:

函数F在(0, 0)的两个偏导数都存在且为0,现在用反证法证明函数F在点(0, 0)不可微。假设函数F在原点可微,则根据可微定义,下列极限必存在,但是下列极限可以通过列举两条路径很容易验证不存在,原假设错误,所以可偏导不一定可微。
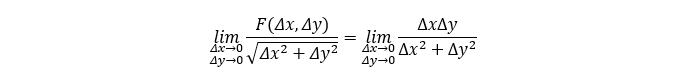
3.2 可偏导不一定连续
在二元函数关系图中,另外一个很让人费解的地方,是二元函数在某点的两个偏导数都存在,但是函数在这一点却不一定连续。为了说明这一点,请看下面这个函数:

相信大家都能很熟练地计算出函数F在原点对x、y的偏导数均为0,但是当曲线沿着y=x的路径趋于原点时,函数值会趋于1,不等于0,因此函数F在原点不连续。
从抽象的角度看,二元函数在某一点的两个偏导数都存在,只能说明二元函数沿x方向、沿y方向趋于该点的值等于函数在该点的定义值,但无法保证沿其它方向趋于该点的值也等于函数值。
转载自:http://www.sohu.com/a/313306970_120115175


评论前必须登录!
立即登录 注册