Concave与Convex函数的区分

最简单的辨识方法

最简单也是最直观的辨识方法是，如果曲线的凹凸部位位于两点连接的直线（即下图中的紫色线）下方，则为convex函数（如下图所示）。

如果曲线的凹凸部位位于两点连接的直线（下图中的紫色线）的上方，则为concave函数（如下图所示）。 口诀总结为 “上cave下vex （上C下V）”。

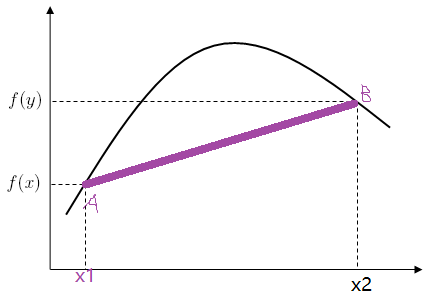
Convex函数

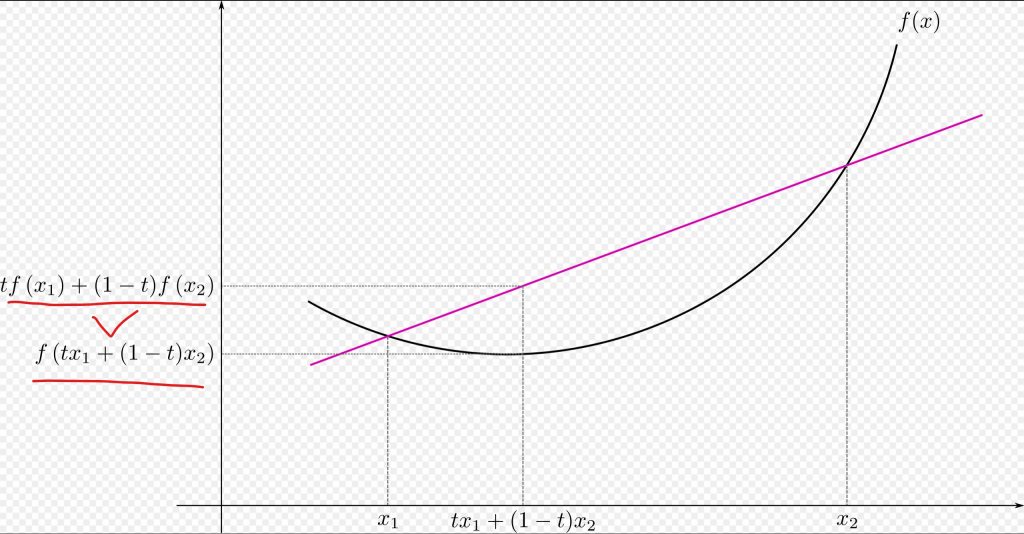
上面是convex与strictly convex函数的定义，下图为convex函数的图像示意：（为了便于理解，可以把下图中的t设置为50%，则 tf(x1) + (1- t)f(x2) = 紫线在与f(x)曲线的两个交点之间紫线的中点位置。tx1+ (1-t)x2 = 横轴上x1与x2之间线段的中点位置。因此很明显，f ( tx1+ (1-t)x2 )＜ tf(x1) + (1- t)f(x2) 。符合上面的convex函数的定义，因此该图像对应着的是convex函数的图像。

Concave函数

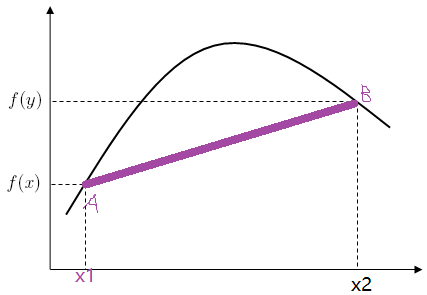
上面是concave与strictly concave函数的定义，下图为concave函数的图像示意：（为了便于理解，可以把下图中的t设置为50%，则 tf(x1) + (1- t)f(x2) = 紫线在与f(x)曲线的两个交点A、B之间的中点位置。tx1+ (1-t)x2 = 横轴上x1与x2之间线段的中点位置。因此很明显，f ( tx1+ (1-t)x2 )＞ tf(x1) + (1- t)f(x2) 。符合上面的concave函数的定义，因此该图像对应着的是concave函数的图像。