本文内容来源于博迪投资学中文第10版的第149-151页,“附录6A 风险厌恶、期望效用与圣彼得堡悖论”相关内容。在此,博主谈谈对这部分内容的理解。以下为原书书影。
该问题的核心解答是人们对于每一单位新收益的边际效用是递减的(特别是,他们的财富越多,对每额外增加的美元赋予的“价值评级”就越少),意味着随着游戏次数的增加,每一单位新的收益所带来的效用不断递减,最后几乎为0,所以当游戏次数趋于无穷,总效用也会趋于一个稳定值,而不是无限增长。因此将这个稳定的效用值转换成他的效用函数里所对应的金额,就是这个玩家所愿意付出的最高门票金额,因为只有当U(门票钱)<U(游戏所得收入)时,他才会去玩这个游戏。这样对玩家来说才有利可图。一旦当U(门票钱)>U(游戏所得收入),他不会去参加这个游戏,他宁愿攥着本来用于购买门票的钞票回家睡大觉,也不想去参加这个游戏了。因为这时在效用上,他是亏本的。
所谓“悖论”,是因为根据计算,这个游戏的收益是随着游戏次数的增加而无限制增长的,所以人们按理说应该无限制地把这个游戏玩下去的,但是实际生活中,人们一般玩上几次就不玩了,所以这造成了一个矛盾的存在,这就是所谓的悖论。原因是每次玩,门票费用也是在增加,因此人们不会无限制地玩下去的。


上面有句话很难理解,就是为啥说“这个游戏的主观效用值确实是有限的,等于0.693”。这句话的意思是,玩一次这个游戏就能扔到正面的期望效用值为(1/2)*ln(2^0),玩两次这个游戏才能扔到正面的期望效用是(1/2^2)*ln(2^1), 玩3次这个游戏才能扔到正面的期望效用是(1/2^3)*ln(2^2)。
所以,预期报酬为:
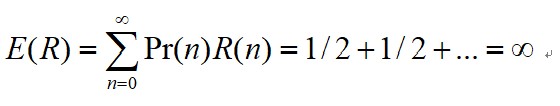
一个特殊的函数ln(R)分配给报酬为R美元的投资者一个主观的价值,报酬越多,每个美元的价值就越小。如果以这个函数衡量财富的效用值,那么这个游戏的主观效用值确实是有限的,等于0.693,即:
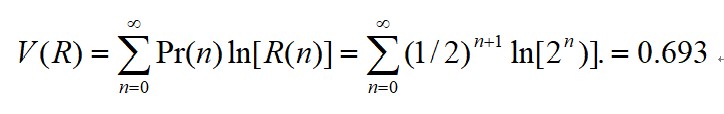
获得该效用值所必须的财富为2美元,因为ln(2)=0.693,因此风险报酬的确定等价物为2美元,也是投资者愿意为游戏付出的最高价钱。
以上内容详细叙述了“圣彼得堡悖论”的来龙去脉。这个问题的核心是探讨游戏参与者愿意为玩这个游戏所付出的最高价钱是多少。下面的例子讨论了“风险厌恶”的基本原理和公平博弈。
关于风险厌恶者,风险喜好者和风险中性者的对比,详见本博客的另一篇文章:风险厌恶者,风险中性者和风险喜好者的区别

下面的内容详细讨论了风险厌恶和期望效用的关系。


在这里主要谈一下文章最后一部分,最后一段里,为什么说“投资者认为稳拿的86681.87美元与有风险的100000美元的效用值相等”。
因为这里计算的风险投资的期望效用11.37,即:

这个11.37,是这种游戏本身所值的效用值,它也并不是独立于游戏玩家之外的客观存在。决定它的大小的因素来源于游戏玩家的心理偏好。大家可以看到,这个11.37在一条笔直的斜线的中点处,这条斜线的两个端点则都在游戏玩家的自身效用曲线上,在中点则意味着这个11.37是一个算数平均值,是这两个端点的平均值。因此,11.37并不是单纯由玩家的效用函数生成的效用值。它虽然与把
86681.87美元带入效用函数(即ln(86681.87美元)=11.37效用)所得到的效用的结果相同,但是它的来源并不是来自于86681.87美元,而是来源于 0.5*ln(50000)+0.5*ln(150000)=11.37 。换言之,它来自于公平博弈游戏所带来的两种游戏结果的效用的平均值。这颇有点“青出于蓝而胜于蓝”的味道。11.37出之于50000美元的效用值和150000美元的效用值的平均值,它源于效用函数,而又不同于效用函数所生成的效用值。
那么11.51又是啥呢?
这里的11.51,是ln(100000)的计算结果,如下所示:

这是将100000美元的财富放置于玩家自身效用曲线上所得到的效用值,换言之,玩家不是把这100000美元投于玩这个公平博弈游戏, 而是持有这100000美元啥都不干所带来的“快感”值11.51。所以在这种情况下,在效用函数为凹函数的情况下(即随着财产数量的增加,每个单位的价值递减;关于为什么风险厌恶者的效用函数为凹函数,参见风险效用函数)。
换言之,玩家选择不参加这个玩心跳的游戏,而是手握这100000元钱在家躺着睡大觉的效用值为11.51,而选择参加这个胆战心惊的游戏,所获得的期望效用为11.37(即平均来说,参加这个游戏所获得的效用值为11.37)。那么,结果一目了然了。也即是说,在风险厌恶者看来(即效用函数为凹函数的人看来),玩这个游戏一点儿也不划算,效用值还不如不玩这个游戏,而选择躺在家里睡大觉的效用值高。所以说,风险厌恶者不会参加公平博弈。
这里的11.37同时位于一条斜率确定的斜线的中点上,也就是说,11.37是一个算数平均值,是ln(50000)与ln(150000)的平均值,也就是平均来说,玩这个公平博弈游戏所能收获的效用值为11.37。
那么现在还有一个问题,那就是算出了平均来说,玩这个公平博弈游戏所可能获得的效用值为11.37,那么把这个11.37置于玩家自身的心里偏好曲线,即这个凹函数曲线上,此时ln(Wce)=11.37,所对应的财富值为Wce=e的11.37次方=86681.87美元。注意,这个11.37的效用值意味着,玩家选择不玩游戏,而是手里攥着86681.87美元去睡大觉的效用值是11.37,它等于玩家选择铤而走险,拿着100000美元去参加这个令人心跳不止的公平博弈游戏所带来的平均效用值。也就是说,玩家选择手里攥着86681.87美元在家里躺着睡大觉的效用与拿着100000美元去参加公平博弈游戏所获得的效用是相等的。
所以书本中最后一句话才会说道 “投资者认为稳拿的86681.87美元与有风险的100000美元的效用值相等 。因此,对他来说二者没有什么区别。”
结尾附上著名华裔经济学家黄有光教授于1965年发表的推翻“阿罗不可能定理”的论文。 Ng, Yew-Kwang (1965). “Why Do People Buy Lottery Tickets? Choices Involving Risk and the Indivisibility of Expenditure”
Kwang-1965-Why-do-people-buy-lottery-tickets-c

评论前必须登录!
立即登录 注册