三角函数是数学中属于初等函数中的超越函数的函数。它们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。
定义式
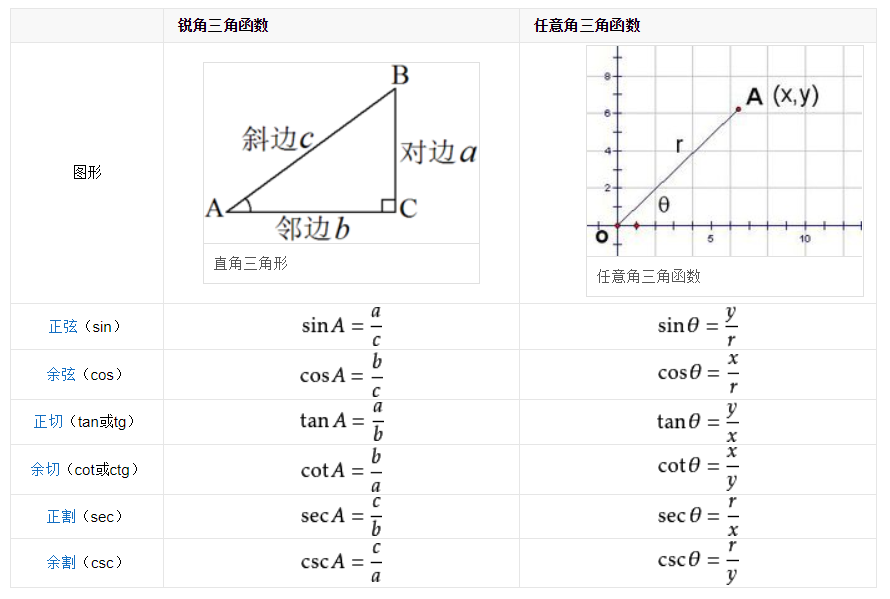
函数关系
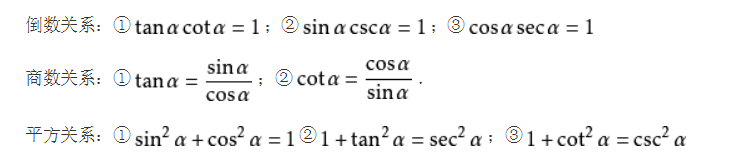
诱导公式
公式一:设 α为任意角,终边相同的角的同一三角函数的值相等:

公式二:设 α为任意角, π+α 与α 的三角函数值之间的关系:

公式三:任意角 -α 与α 的三角函数值之间的关系:

公式四:π -α 与α 的三角函数值之间的关系:

公式无:2π -α 与α 的三角函数值之间的关系:

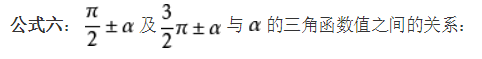

记背诀窍:奇变偶不变,符号看象限.即形如(2k+1)90°±α,则函数名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。形如2k×90°±α,则函数名称不变。
诱导公式口诀“奇变偶不变,符号看象限”意义:
k×π/2±a(k∈z)的三角函数值
(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;
(2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。
记忆方法一:奇变偶不变,符号看象限:

记忆方法二:无论α是多大的角,都将α看成锐角:
以诱导公式二为例:
若将α看成锐角(终边在第一象限),则π+α是第三象限的角(终边在第三象限),正弦函数的函数值在第三象限是负值,余弦函数的函数值在第三象限是负值,正切函数的函数值在第三象限是正值。这样,就得到了诱导公式二。
以诱导公式四为例:
若将α看成锐角(终边在第一象限),则π-α是第二象限的角(终边在第二象限),正弦函数的三角函数值在第二象限是正值,余弦函数的三角函数值在第二象限是负值,正切函数的三角函数值在第二象限是负值。这样,就得到了诱导公式四。
基本公式
1. 和差角公式
二角和差公式


三角和公式



2. 和差化积公式

和差化积公式记忆口诀:
正加正,正在前;
余加余,余并肩;
正减正,余在前;
余减余,负正弦.
3. 积化和差公式




4. 倍角公式
二倍角公式

三倍角公式





5. 半角公式


6. 万能公式

7. 辅助角公式

其他公式
1. 正弦定理
在任意△ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R.则有:

正弦定理变形可得:

2. 余弦定理

对于如上图所示的边长为a、b、c而相应角为α、β、γ的△ABC,有:

也可表示为:

3. 降幂公式
sin²α=[1-cos(2α)]/2
cos²α=[1+cos(2α)]/2
tan²α=[1-cos(2α)]/[1+cos(2α)]
4. 万能公式

本文参考自如下网站,有改动
https://baike.baidu.com/item/%E4%B8%89%E8%A7%92%E5%87%BD%E6%95%B0%E5%85%AC%E5%BC%8F/4374733


评论前必须登录!
立即登录 注册