子博弈完美纳什均衡（subgame perfect Nash equilibrium）
https://wiki.mbalib.com/wiki/%E5%AD%90%E5%8D%9A%E5%BC%88%E7%B2%BE%E7%82%BC%E7%BA%B3%E4%BB%80%E5%9D%87%E8%A1%A1
ppwq扩展形式的博弈（Extensive-form game）
https://zh.wikipedia.org/wiki/%E6%89%A9%E5%B1%95%E5%BD%A2%E5%BC%8F%E7%9A%84%E5%8D%9A%E5%BC%88
正则形式的博弈（Normal form game）
https://wiki.mbalib.com/wiki/Normal_Form_Game
奇函数和偶函数在对称区间积分的特点
奇函数在对称区间上积分为零，偶函数在对称区间上积分等于它在整个区间的一半上的积分的2倍。 比如，对于y=x^3,它为奇函数，对于任何一个以原点对称的区间（-a，a）(a>0)上积分为零。 而y=cosx为偶函数，它在任意对称区间（-a，a）...
奇函数乘以偶函数，结果为奇函数
奇函数 × 偶函数= 奇函数 奇函数 × 奇函数= 偶函数 偶函数 × 偶函数= 偶函数 奇函数÷偶函数=奇函数 奇函数+偶函数结果既不是奇函数也不是偶函数 奇函数+奇函数=奇函数 奇函数÷奇函数=偶函数 偶函数＋ － × ÷偶函数=偶函数...
0的阶乘是1，即0！= 1
特别规定，0的阶乘是1，即0！= 1 。
排列公式与组合公式
(一)两个基本原理是排列和组合的基础 (1)加法原理：做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+m3+…...
如何理解多元函数可微与可偏导的关系？
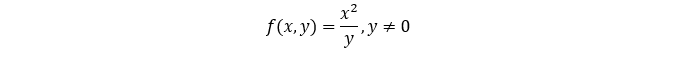
谈到多元函数可微与可偏导时，相信不少人头皮有点发麻。一元函数中，可微与可导是等价的，但是在多元函数中，可微与可偏导之间的关系就没那么简单了，这是为什么呢？本文小编将以二元函数为例进行详细的说明。 1.二元函数的可偏导 在二元函数中，一元函数...
不定积分中的常见公式
(secx) ‘ = secxtanx (tanx) ‘ = sec²x sec²x = 1 + tan²x (arcsin x) ‘= 1/ (1- x²) (arccos x) ‘ = -...
微分符号dx, dy 的含义
d意思是 differential（微分）的意思，相当于把d后面的数值无限等分，比如dx就是对x进行无限等分，又因为f'(x) 是x每增加一点点所带来的y的变化率，也就是dy = f'(x) dx, 从而有dy/ dx = f'(x)。 -...
