数学 第5页

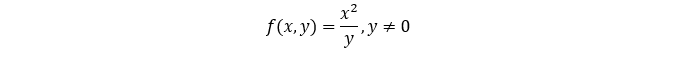
谈到多元函数可微与可偏导时，相信不少人头皮有点发麻。一元函数中，可微与可导是等价的，但是在多元函数中，可微与可偏导之间的关系就没那么简单了，这是为什么呢？本文小编将以二元函数为例进行详细的说明。 1.二元函数的可偏导 在二元函数中，一元函数...

赞(1)ppwq2019-10-02阅读(4575)去评论

(secx) ‘ = secxtanx (tanx) ‘ = sec²x sec²x = 1 + tan²x (arcsin x) ‘= 1/ (1- x²) (arccos x) ‘ = -...

赞(1)ppwq2019-09-26阅读(2600)去评论

d意思是 differential（微分）的意思，相当于把d后面的数值无限等分，比如dx就是对x进行无限等分，又因为f'(x) 是x每增加一点点所带来的y的变化率，也就是dy = f'(x) dx, 从而有dy/ dx = f'(x)。

赞(1)ppwq2019-09-24阅读(13841)评论(2)

例子： 求如下函数的导数： 我们有 y’ =

赞(0)ppwq2019-09-23阅读(1631)去评论

汤家凤在2020版大学高数同步视频课程中亲口说道，o (x^3) – o (x^3) = o (x^3) 。见笔记P97。 https://jingyan.baidu.com/article/b24f6c82207db186bf...

赞(3)ppwq2019-09-22阅读(6738)去评论

若lim(β/α)=0，则称“β是比α较高阶的无穷小”。意思是在某一过程(x→x0或x→∞这类过程)中，β→0比α→0快一些。 基本概念 无穷小的量的比较 常用的等价无穷小

赞(0)ppwq2019-09-22阅读(4757)去评论

在应用洛必达法则解 0^0 型极限时，应当立即想到 e^(ln2)=2 这个等式。比如，在计算x趋向于0+时，x^sinx的极限时，应当首先将x^sinx等价转化为e^ln(x^sinx)的形式，又因为 ln(x^sinx)=sinx*ln...

赞(0)ppwq2019-09-13阅读(3171)去评论

先说判断某一个点上函数连续的方法：从这个x值的两侧，函数的左右极限都等于函数在这个x点上自己本身的函数值，那么函数在这个x点上就连续了。（我们默认左右两个单侧极限都存在哦） 其实有一种形象的理解：对于一个给定的x点，函数从该点左右两侧分别无...

赞(0)ppwq2019-09-12阅读(1264)去评论

https://www.ixueshu.com/document/5131f8778c99f76d14a4dc030e7d94c3.html#pdfpreview

赞(0)ppwq2019-09-12阅读(1095)去评论

反三角函数是一种基本初等函数，它包括反正弦函数、反余弦函数、反正切函数以及反余切函数的求导。 反正弦函数的求导：(arcsinx)’=1/√(1-x^2) 反余弦函数的求导：(arccosx)’=-1/√(1-x^2...

赞(1)ppwq2019-09-11阅读(2898)去评论